گفتگوهایی درباره نقد ریاضیات: قسمت سوم، نقد و تشویق تحقیقات در جبر

امیرحسین اکبرطباطبایی، آرش رستگار، سید محمدرضا موسوی، محمدحسین نادری

پیاده‌سازی و بازنویسی: سیدمحمدرضا موسوی

گفتگوهایی درباره نقد ریاضیات: قسمت سوم، نقد و تشویق تحقیقات در جبر

امیرحسین اکبرطباطبایی، آرش رستگار، سید محمدرضا موسوی، محمدحسین نادری

پیاده‌سازی و بازنویسی: سیدمحمدرضا موسوی

آرش رستگار- مرور آنچه گذشت: عرض شود که ما تا حالا دوتا «گفتگوهایی درباره ریاضیات» داشتیم که دومی‌اش «نقد و تشویق تحقیقات در ترکیبیات» بود؛ که آنجا قرار بود من سه شاخه خوب یا گرایش خوب در ترکیبیات که می‌پسندم را بگویم که اینها خوب دارند ترکیبیات انجام می‌دهند، و چرا خوب است،  و سه تا چیزی که نمی‌پسندند بگویم و توضیح بدهم که چرا خوب نیست، و دکتر اکبرطباطبایی هم قرار بود که اصلاح کنند و فرمان بدهند. بگویند چه چیزهایی را خوب نگفتم، یا دوباره بگویم یا اینکه یک ذره توضیحات اضافی بدهند یا اینکه بگواند فلان مورد قبول نیست و پذیرفته نیست و اصلاح کنیم و  مدیریت کنیم. عین همان کاری که در« نقد و تشویق تحقیقات در ترکیبیات» انجام دادیم.

منتهی من بخواهم یک مروری کنم، این بود که ما جبر و هندسه و آنالیز و ترکیبیات را روی یک چهاروجهی قرار دادیم و این را گفتیم که جبر و ترکیبیات در واقع نیمه گسسته ریاضیات هستند، در برابر هندسه و آنالیزی که نیمه پیوسته ریاضیات هستند. همین‌طور جبر و آنالیز نیمه کلامی ریاضیات هستند، و هندسه و ترکیبیات نیمه تصویری ریاضیات. و قرار بود که بین این شاخه‌ها جریان‌های موازی وجود داشته باشد که ما در کارهای‌مان با آنها سر و کار داشته باشیم، مثلاً یک جوری جبر و آنالیز آنالوگ همدیگر اند منتهی یکی‌شان گسسته انجام دادن همان کارهاست و یکی‌شان پیوسته انجام دادن همان کارها. و باید ما این توازی را در این دو تا شاخه از ریاضی ببینیم. یا  جبر و هندسه، بینشان دوباره یک آنالوژی برقرار است که ریاضیات تصویری با ریاضیات کلامی موازی هم قرار بگیرند و قابل ترجمه به هم باشد. در ترکیبیات و هندسه هم باز یک توازی بود، آنالوژی بود، که قرار بود ترکیبیات ورژن گسسته هندسه باشد و هندسه ورژن پیوسته ترکیبیات. و مثلاً اگه بخوام مثال بزنم، مثلاً در ترکیبیات یک مفهومی در ایران خیلی رواج دارد، می‌شود در نظریه گراف، مفهوم Domination و Minimal Dominating Set. من داشتم با خودم فکر می‌کردم که خب تو اگر می‌خواستی پیوسته انجام بدهی چگونه انجامش می‌دادی؟ بعد گفتم که خب اگر من می‌خواستم این را پیوسته انجام بدهم، می‌دیدم آیا در عالم پیوسته چیزی شبیه به این هست یا نه؟ بعد دیدم عه! این مسئله موزه که شما یک موزه چندضلعی دارید و کمترین تعداد دوربین که همه جا را ببینند می‌خواهید، مسئله پیوسته‌ای است دیگر. بعد دیدم چه جالب، اون موزه هم یک گراف است در واقع، ولی رئوسش همه نقاط مرزی هستند. و یال‌هایش هم این پرتوهای نور اند و هم رأس‌ها پیوسته حرکت می‌کنند، و هم پرتوهای نور پیوسته می‌توانند حرکت کنند. بعد دیدم که خب این پرتوهای نور در موزه خیلی شبیه به بیلیارد هستند؛ بعد گفتم بیلیارد هم پس یک گراف است که شما توپ را می‌زنید یک جایی و برمی‌گردد. و بعد گفتم پس این هم شد یه ورژن پیوسته‌ای از اون موجودات که شبیه موجودات گسسته بودند. بعد گفتیم که حالا چگونه این بیلیارد را برگردانیم در گراف؟ گفتم خب توپ که می‌خورد جایی و برمی‌گردد، در واقع یک تابعی می‌دهد از مرز به خودش که اون نقطه را می‌برد به خودش، ولی هر نقطه دیگر مرز را می‌گوید که بعد از خوردن به اون نقطه به کجا می‌رود؛ و پس یک تابع مرتبه دوم می‌شود، یک involution می‌شود. یک اینولوشن است برای هرنقطه‌ای. مثلاً برای نقطه x که روی مرز است، اینولوشن ϕx داریم که b را می‌برد به ϕxb و ϕxb را می‌برد به b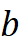.  اگر در هر رأس این‌چنین اینولوشنی داشته باشیم در واقع یک بیلیارد داریم. خب در گراف دلخواه هم شما می‌توانید در هر راسی آن چیزهایی که خارج می‌شوند را به‌طور موضعی روی‌شان یک تابع مرتبه دو تعریف کنید، که اگر از اینجا آمدی، از آن یکی خارج می‌شوی، و اگر از آنجا آمدی داخل، از این یکی می‌روی بیرون؛ و می‌شود یک بیلیارد. و بعد گفتم خب اینجا که اون نورها درش نیستند دیگر، اصلا درون ندارد که! پس دوباره برمی‌گردم به پیوسته، یک ورژن دیگر از بیلیارد درست می‌کنم که می‌گوید شما روی هرنقطه‌ای، یک منیفولد دارید که همان مرز است؛ داخل بیلیارد هم دیگر هیچی نیست. در هر نقطه از منیفولد مثل نقطه p، یک اینولوشن ϕp دارید. اینولوشن ϕ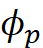p که p را ثابت نگه میداره و  بقیه نقاط را تغییر می‌دهد، مرتبه‌اش هم دو است. خب حالا اگه a را شوت کنیم به b آن وقت ϕba اون چیزی است که بعد از b می‌خورد بهش. یعنی مثلاً ϕba می‌شود c. حالا b بخورد به c به کجا می‌رسد؟ باید ϕcb را در نظر بگیریم. بعد دکتر نصیری به من کمک کرد که این را می‌شود به زبان سیستم‌های دینامیکی ترجمه کرد. اول گفت خب این یک نگاشتی است از M×M به M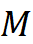 که a,b را می‌بره به ϕba. بعد من گفتم که ما می‌خواهیم از فضا به خودش باشد، گفت اشکال ندارد M×M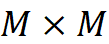 را ببریم به M×M و a,b را ببریم بهb,ϕba. 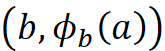و اون وقت دینامیک است. دوباره یک سیستم دینامیکی می‌شود که self-map است. خب بنابراین ما الان چه کار کردیم؟ هی از ترکیبیات، از گراف، رفتیم در سیستم‌های دینامیکی، دوباره برگشتیم، دوباره رفتیم، دوباره برگشتیم، و در همه رفت و برگشت‌ها می‌شود رفت دید که آن طرف چه قضایایی داریم و این طرف چه قضایایی داریم، و آن طرف چه شرط‌هایی بگذاریم تا شبیه این قضایا درست بشود؟ چه قضایایی را نمی‌شود درآورد؟ فیچرشان چه بوده؟ همه اینها باعث فهم بهتر می‌شود. و خیلی خوب است که ما بتوانیم هم بین جبر و هندسه چنین رفت و برگشتی درست کنیم، و هم بین جبر و آنالیز چنین رفت و برگشتی درست کنیم. و سعی‌مان این است که اینجا این‌چنین کاری را بکنیم. حالا من یک «سه به علاوه سه» جبر می‌خواهم معرفی کنم، که آن سه تایی که می‌خواهم تشویق کنم یکی کارهای «دوروف» است، یکی مفهوم Algebraic Operad و یکی هم Higher Algebra، ببینم اصلاً چقدر فهمیدم. و اون سه تایی که می‌خواهم نقد کنم آن طوری‌ست که در عصر ما جبر، جبر جابجایی، انجام می‌دهند و آن طوری که جبر ناجابجایی انجام می‌دهند و آن طوری که نظریه گروه‌ها انجام می‌دهند. یعنی تحقیقات در حلقه‌های جابجایی و حلقه‌های ناجابجایی و نظریه گروه‌ها؛ به اینها می‌خواهم انتقاد کنم. حالا سعی می‌کنم جوری انتقاد کنم که انتقادهایم تکراری نباشد.

آرش رستگار- سوال راجع به رفت و برگشت: جناب نادری می‌پرسند که شما فرض کنید بین ترکیبیات و هندسه رفت و برگشت کردیم و قضیه این‌ور را برداشتیم رفتیم آنجا، بهترش کردیم، فیچرش را فهمیدیم، دوباره برگشتیم، دوباره رفتیم، یک سری قضیه ثابت شد. حال ممکن است یک ریاضی‌دان فکر کند که اصلا gain همین است و ما هی می‌خواهیم قضیه ثابت کنیم؛ و سؤال اینه که آیا این‌طوری همه ریاضیات را می‌شود بدست آورد یا نه؟ عرض شود که اولاً بله درست است، همون‌طور که گفتید gain این نیست که ما هی قضیه ثابت کنیم. بلکه اینها باید motivated باشند به چندین معنی؛ یعنی در بستر یک تئوری باشند که آن تئوری برای حل یک سوال‌هایی است و یک نگاه پرسشگر بلند مدتی هست، تکلیفش با شناخت ما، تأثیری که بر شناخت ما می‌گذارد معلوم باشد و تکلیفش با حقایقی که دنبالش می‌گردیم و می‌خواهند متجلی بشوند در دو طرف معلوم باشد. و در واقع ما داریم سعی می‌کنیم حقیقتی که در دو طرف متجلی شده است را با کمک این آنالوژی‌ها بهتر و بهتر بشناسیم؛ و علامت بهتر شناختن هم این است که دو طرف آنالوژی را بهتر و بهتر می‌شناسیم. در واقع کاری که داریم می‌کنیم توسعه نظریاتی است که باهم آنالوگ هستند، با استفاده از این آنالوژی بین دوتا پارادایم مختلف، بین دوتا زمین بازی مختلف حرکت می‌کنیم. و سؤال این است که آیا همه قضایای ریاضی که می‌شود ثابت کرد به این صورت می‌شود ثابت کرد؟ یا نه کارهای دیگری هم باید بکنیم؟ عرض شود که پاسخ این است که اولاً هدف ما این نیست که همه قضایی که می‌شود ثابت کرد را پیدا کنیم، چون خیلی چیزهایی که درست هستند برای ما معنی‌ای ندارند، تأویلی ندارد، نمی‌توانیم به زبان حقیقت ترجمه‌اش کنیم، لااقل امروز. بنابراین هدف این نیست که هی قضیه ثابت کنیم، هدف این است که آن پارادایم‌های دو طرف را عمیق بشناسیم؛ یعنی چه؟ یعنی ما می‌خواهیم یک گزارشی بدهیم بگوییم ما این دوتا سرزمین را داریم مطالعه می‌کنیم در مقایسه با هم، و  نمی‌آییم مثلاً بگوییم من این‌کار را کردم این قضیه ثابت شد،  آن کار را کردم آن قضیه ثابت شد، و قضیه‌هایمان را کنار هم و پشت سر هم بگذاریم بشود پیپر! ما در مقالات‌مان از یک سرزمین ناشناخته که به آن سفر کردیم با سرزمین مادری‌مان داریم مقایسه می‌کنیم و گزارش می‌دهیم که بگوییم آنجا چه خبر بود و مثلاً می‌توانیم بگوییم زیر زمین‌شان گوهر داشتند، معدن فیروزه هم داشتند، ولی قرار نیست دانه دانه همه فیروزه‌هایش را رده‌بندی کنیم و اینها را مثلاً انبار کنیم برداریم ببریم آن‌ور! ما داریم با مقایسه دو طرف، حقیقت را می‌فهمیم. کلکسیون درست کردن، چه از مفاهیم، چه از قضایا، و چه از مثال‌های زیبا، لزوماً تقدس ندارد.

آرش رستگار- کارهای دوروف: عرض شود که داستان اول که می‌شود اولین نوع جبر انجام دادنی که من می‌خواهم تشویقش کنم، دوباره بحثی است که قبلاً هم کرده‌ایم. ولی خب من الان به عنوان «سه به علاوه سه» دارم می‌گویم، ریاضیات «دوروف» است. و می‌خواهم بگویم که چرا من کارهای دوروف را دوست دارم و مهم است و این‌طور جبر انجام دادن درست است. کاری که دوروف می‌کند اولاً یک فرمالیسم است که عین نظریه شماهای گروتندیک، اسکیم تئوری، بین جبر و هندسه یک توازی به وجود میاورد ولی آن جبری که دوروف دارد با آن کار می‌کند در واقع موجوداتش کتگوری‌ها هستند نه یک مجموعه از اعضاء که اپراتوری روی‌شان تعریف می‌شود. بنابراین درواقع جبر را بالا برده است از آن چیزی که زمان هیلبرت می‌گفتند به آن دنیایی که آینبرگ و مکلین و نهایتاً گروتندیک درست کرده‌اند. این یک جور بالا آوردن این جبر است. حالا من آن چیزهایی که می‌فهمم را می‌گویم، شما بعد بهترش کنید. عرض شود که دوروف کسی است که تلگرام را ساخته و دانشجوی دکترای فالتینگز بوده است. خیلی حساس بوده، فالتینگز هم مثل همه تحویلش نگرفته، و او ریاضیات را ول کرده و بعد رفته تلگرام را ساخته. ریاضیات دوروف در واقع همون تز دکترایش است که خیلی هم کلفت و غنی است. در واقع یک ذره کارهای توئن را پیش برده که  توئن برای مونوییدها سعی می‌کرده است ریاضی انجام بدهد، که میدان یک عضو هم جزوش بوده، دوروف اینها را می‌آورد روی مونادها پیاده می‌کند. که اینها برای جفتشان باید کتگوری بدانید؛ که مونویید یعنی چی، موناد یعنی چی. شما برای سادگی الان می‌توانید بگویید مونویید همان نیم‌گروه است، ولی خب این‌طور نیست اصلاً. باید خیلی کتگوری تئوری فهمید که بفهمیم منظور از مونوییدی که توئن می‌گوید چیست. ولی دوروف یک بعد از اهمیت کارهایش این است که چندین ریاضیات را به هم متصل می‌کند. چندین مسئله و چندین شاخه مهم ریاضی را به هم متصل می‌کند که این شاخه‌ها آراکلوف تئوری باشند، بعد tropical geometry باشند، field with one element باشند، و هندسه جبری معمولی، اسکین تئوری و این‌ها باشند. امیدوارم چیزی جا ننداخته باشم. بنابراین چندین مسئله باستانی را، عین کار نیوتن، که حسابان را درست کرد، با هم متحد کرد. بنابراین این بیشتر از یک چیزی مثل فیلدز و این‌هاست، بلکه او را در حد بزرگ‌ترین ریاضیدان‌های تاریخ می‌تواند قرار بدهد. یک نکته دیگری که جالب است، میاید در آراکلوف تئوری می‌گوید که شما به جای آنالیز بیایید جبر بگذارید؛ به جای اون هندسه و آنالیزی که، آنالیز هندسی‌ای که، در پرایم بی‌نهایت هست میاید یک ورژن جبری همان موجودات را قرار می‌دهد که خیلی قشنگ است. در جهت این فلسفه کلی که شما روی همه پرایم‌ها یک جور ریاضی انجام می‌دهید، پرایم در بینهایت را برمیدارید یک جور دیگر ریاضی انجام می‌دهید. مثلاً در Function Field همین‌کارهای آراکلوف تئوری را برای همه پرایم‌ها یک جور انجام می‌دهید، یک پرایمی را روی curve تان می‌گیرید بی‌نهایت، برای آن دوباره  میایید یک جور دیگری، مثلاً با Non-Archemedian Algebraic Geometry، آراکلوف تئوری انجام می‌دهید. و تلاش‌هایی هم در این جهت شده. و بعد میایید Intersection Theory تعریف می‌کنید مانند این. بعد آن وقت یک مقایسه‌ای پیش میاید بین روش آراکلوف و روش دوروف، که دوروف می‌گوید آن چیزهایی که از لحاظ هندسی ساده اند، مثلاً smooth algebraic curve در بی‌نهایت می‌شوند، از لحاظ algebraic خیلی فرمول بندی‌شان پیچیده می‌شود در فرمول‌بندی دوروف. و آن چیزهایی که از لحاظ جبری ساده اند، از لحاظ هندسی singular و پیچیده و عجیب و غریب می‌شوند. و این اصلاً خودش یک پدیده‌ای در ریاضیات است، و این خیلی مهم است که کسی جبر را طوری انجام بدهد که چنین پدیده‌هایی خودشان را نشان بدهند. و آراکلوف تئوری با همه‌جای ریاضیات سر و کار دارد. هندسه درش دارد، جبر دارد، آنالیز دارد، ترکیبیات دارد. و کسی که دارد جبر انجام می‌دهد، که دوروف باشد، با همه اینها دارد در جبر مدل می‌کند. اصلاً جبر سرچشمه‌اش شاخه‌های دیگر ریاضی‌اند. از اول هم همین‌طور بوده است. نظریه اعداد هم همین‌طور است. ایده می‌گیرد، مجرد می‌کند، بعد تعمیم می‌دهد به جاهایی که آن ایده‌ها دیگر کار نمی‌کنند. خوبی دیگری که دوروف دارد این است که، همین‌که در یک نقطه بر می‌داریم یک جور دیگری انجام می‌دهیم، این آنالوگ p-adic هم دارد. در پرایم‌ها هم ما می‌توانیم در یک پرایمی p-adic Analysis انجام بدهیم. و این نکته جالبی است که p-adic Analysis جبر است، نظریه اعداد نیست. البته قبلاً برای دکتر طباطبایی جدا گفته‌ام، ولی چون اینجا باید بیاید این را توضیح بدم که مثلاً آن کارهایی که p-adic است و p-adic Analysis درش دارد،  مثل کارهای شولتزه و اینها، Arithmatic نیست؛ Arithmatic درواقع Z است؛ درست است که اعداد p-adic در نظریه اعداد هستند، ولی مشابه R اند. و نشان به همان نشان که می‌خواهند یک کارهایی در آنالیز تابعی را برای p-adic بکنند نمی‌شود، یک روش‌های جدیدی پیدا کردند بعد فهمیدند در آنالیز تابعی معمولی هم این کارهای جدید را می‌شود کرد، که شده کارهای جدید شولتزه. اینها را برای من آقای پرتوفرد تعریف کرده است. و بنابراین دارد می‌گوید که اعداد p-adic هم یک جور جبر انجام دادن است. شولتزه هم یک جور جبر انجام دادن است. و بعد همه اینها با این جور جبر انجام دادن با آنالیز انجام دادن هم ارتباط رفت و برگشتی دارد. شولتزه این ارتباط رفت و برگشتی را نشان می‌دهد. آراکلوف تئوری این ارتباط رفت و برگشتی را نشان می‌دهد، چون آنجا با آنالیز منیفلد در بینهایت سر و کار داریم، و جالب این که نقش آنالیز را دوروف با جبر جایگزین می‌کند و می‌گوید که می‌شود. و بعد هم آن فیچری که می‌گوید بعضی از حقایق تجلیات هندسی‌شان پیچیده‌ست ولی تجلیات جبری شان ساده است و برعکس. اینها نکاتی بودند که راجع به دوروف می‌خواستم بگویم. یک کمی هم توضیح بدهم. در جبر اینکه شما با شاخه‌های دیگر ارتباط داشته باشید خیلی مهم است. یک جایزه‌ای در جبر هست، در جبر و  نظریه اعداد، اسمش جایزه Cole است. بعد آنجا می‌رویم می‌بینیم همه کسانی که جایزه Cole را گرفته‌اند، آدم‌هایی هستند که دارند بین رشته‌ای، رابطه جبر را با یک شاخه دیگر دنبال می‌کند. و این‌طور نیست که بیایند شاخه جبر را به عنوان یک شاخه‌ای که از لحاظ فلسفی مستقل از سرچشمه‌هایش است و با یک نگاه اصلی موضوعی، که حالا ببینیم چه در میاید، انجام بدهند. من نقدهایی که می‌خواهم به مثال‌های بعد جبر مطرح بکنم، نقدهایی از همین جنس خواهد بود که عرض کردم.

آرش رستگار- operads: این بخش در رابطه با operads هست؛ یک اشتراکاتی با دروف داره خوبی‌های operad ولی یه ذره غلیظ‌تر. یک سو اینکه مفهوم topological operads به هندسه تکیه می‌زنه و تعبیر هندسی از عملیات جبری می‌ده و از ترکیب توابع ایده می‌گیره، چون یه جور عمل ترکیبه، حالا ترکیب  توابع نیست ولی این تعبیر هندسی به ما عمیق‌تر میفهمونه که توی جبر داریم چه چیزی رو مدل می‌کنیم و ربطی که بین topological operad و algebraic operad هست، به این معنی که شما بیاین گروه هومولوژی topological operad را بگیرید، به اندازه کافی ربط عمیقی نیست و مفهوم algebraic operad و topological operad به طور ذاتی به هم ربط دارن. توی فرمول‌بندی دروف از جبر هم می‌شه اینارو باز چید، و توی higher algebra هم که بعد راجع بهش صحبت می‌کنم بازم می‌شه مفهوم operad رو دید که داخل می‌شه. تعریف کردن یک operad، یعنی چیزی که بشه عمل ترکیب روش گذاشت به خصوص به صورت هندسی، این تمرین خیلی خلاقانه‌ای محسوب می‌شه و باعث می‌شه که عمل ترکیب رو آدم بفهمه. من چند تا operad خودم تعریف کردم از جمله اینکه شما یک مربع می‌گیرین که k تا نقطه در آن  هست که سطر و ستون هاشون دوبه‌دو متمایزه، و بعد k تا مربع شبیه به این می‌تونین تو این نقاط جایگزین کنین که هر کدوم n_i تا نقطه توشون هست، با همین شرایط که سطر و ستون یکی نیست. چجوری جایگزین می‌کنیم؟ برای هر کدوم از این k تا نقطه، مربع رو تو سطر و ستون این نقاط می‌بریم و جای اون نقطه مربع می‌گذاریم بقیه قسمت ها هم که خالی مونده خالی می زاریم. حالا شما می‌تونین برای نظم بیشتر اینکارو بکنین که مربع ها رو واحد بگیرین آخرش مربعی که درست کردیم واحد کنین یا می‌تونین اصلاً نه، مربع هایی که واحد نیستن با هم ترکیب کنین، عین همین کارو توی بُعدهای بالا میشه کرد و این operad که اسمش رو بذارم «سطر و ستونی» رو میشه توی بعد سه یا بعد دلخواه n پیاده‌اش کرد. و بعد این مثال‌ها، شبیه مثالی که من زدم چند تا دیگه هست که تو مقاله‌ای راجع به operad ها توی ReasearchGate گذاشتم، به ما می‌گه که مسئله غنی‌تر از اینی هست که شما با همولوژی و کهومولوژی، operad های topologic رو algebraic کنی؛ و اصلاً فراتر از توپولوژیه، هندسه است مفهوم operad. و اینکه شما این عمل ترکیب رو که از جبر میاد با این شهود هندسی و خلق operad ها و فهمیدن اینها و انجام دادن هندسه به این معنی ترکیب کنی، داره یک نگاه جدیدی به جبر معرفی می‌کنه و یه جور جدیدی از جبر انجام دادن رو در برابر ما قرار می‌ده که نزدیک‌تر است به روش‌های کویلن تا به روش‌های گروتندیک که البته گروتندیک هم به روش کویلن خیلی احترام می‌ذاره. ولی باز کویلن هم توپولوژیست هست، از کویلن هم می‌شه هندسی‌تر شد، کانسیوویچ کارای هندسی راجع به operad داره، و دولین یک حدسی داشته راجع به operads که یه چیزی تو این مایه‌هاست که اپراد little disks فرماله، که یک حدس راجع به ساختار جبری اپراد little disks هست ولی داره نشون می‌ده که چه ساختارهای پشت صحنه‌ای اپرادهای هندسی می‌تونن داشته باشن. یه چیز دیگه که راجع به اپرادها خیلی تکان دهنده‌ست، استرایکینگه، اپراد خم‌های جینس g پوینتد (روشون نقطه انتخاب کرده باشیم مرتب) هستش که با فیزیک ربط داره. اگه جینس رو صفر بگیریم باز هم خم‌های جینس صفر پوینتد که البته سینگولارش هم در نظر بگیریم، تشکیل یک اپرادی می‌دن که این رو observe کرده بودن که اصول موضوعه نظریه زایبرگ-ویتن چیزی جز ساختار اپرادی این فضاها مدولی نیستش. و درک عمیق‌تری که ما از فضاهای مدولی داریم در توپولوژی جبری، بعد از این حدس‌هایی که مامفورد زد و روش‌هایی که توی توپولوژی جبری ابداع شد برای بررسی اونها، فهم عمیق‌تری از اپراد هم می‌تونه به ما بده. یکی از این نکات مهمی که توی اون روش‌هایی که روی moduli space ابداع شده، هست مفهوم infinite loop space هست که حالا من توی قسمت higher algebra به اون اشاره می‌کنم چون اونجا هم وارد می‌شه. Infinite loop space یعنی تمام loop های فضا رو در نظر بگیری، یک فضای جدید بدست میاد، دوباره تمام loop های توی این فضای جدید رو در نظر بگیرین، یک فضای دوم بدست میاد و همین کار رو بی‌نهایت بار ادامه بدیم. با اینکه روی فضاهای بینهایت بعدی بینهایت بار داریم هی بزرگشون می کنیم، و شهود هندسی داشتن که کل نگرانه باشه از همچین فضاهایی خیلی کار سختیه، با این حال اینها به درک عمیق ما از ساختارهای topologic کمک می‌کنن که متأسفانه توی هندسه جبری غایبه. حالا راجع به این صحبت خواهم کرد.

آرش رستگار- higher algebras: خیلی خب. سومین روش انجام دادن جبری که می‌خوام تشویق کنم higher algebra است و بخصوص higher category و به خاطر بخصوص کانکشن‌هایی که باز دوباره با توپولوژی داره و از مسیرهای مختلفی می‌شه با اینا آشنا شد ولی من از کتاب بائِز و مِی از اونجا شروع کردم و یکی از باز مهم‌ترین higher categories و infinite categories از infinite loop space میاد که به نظر من این که شما همچین فرمول‌بندی‌ای رو توی شاخه‌های مختلف پیاده بکنی کار خیلی عمیقی می‌شه و من یه مثالی به نظرم می‌رسه از هندسه جبری که شما اگر یک فضای مدولی رو در نظر بگیرید چیزی شبیه به loop spcae است. یک جور فضای مدولی خم‌های توی فضاست و دوباره یک فضای مدولی دیگه سوار از اون فضاهای مدولی در نظر  بگیرین چیزی شبیه به دو بار loop space گرفتن است. و همین جور می‌شه هی فضای مدولیِ فضای مدولی گرفت تا بشه infinite loop space. یک مثال خاصش توی هندسه جبری مثلاً مپ‌های از یک فضای ساده به یک فضاست که بعد از اینکه فضای مدولی این فضا رو نظر گرفتیم مثلاً می‌تونیم با روش‌های کانسیوویچ stable map ها رو بگیریم که moduli space خوبی داشته باشن. بعد دوباره فضای مدولی map ها از همون فضا به همین فضای مدولی stable map ها در نظر گرفت که بشه طبقه دوم، و همین‌طور تا طبقه بی‌نهایت رفت. این یه نگاهی به ما می‌ده که شما وقتی کتگوری رو بهش به عنوان یک عالمی از اشیا نگاه می‌کنید و کتگوری رو عالمی از عوالم نگاه می‌کنید و همین‌طور عالمی از عوالم از عوالم الخ، به شما می‌گه شاید همان عالم اولی‌تون عالمی از اشیا ریاضی نباشه، عالمی از عوالم باشه؛ که شما اون عوالم رو در اشیا ریاضی خلاصه کردین. بعد فکر کردم ببینم همچین ایده‌ای رو می‌تونم توی یک موجود ساده ریاضی پیاده کنیم و به نظرم حتی توی اعداد طبیعی می‌شه این رو پیاده کرد که شما بگین ۱ یه عالمه، ۲ عالمه، ۳ عالم، مثلاً ۴ عالمه. مثلاً ۲ هم ۲ باشه هم ۱+۱ باشه. ۳ هم ۳ باشه، هم ۱+۲ باشه، هم ۱+۱+۱. حالا شما می‌تونین + رو جابجایی بگیرین یا غیر جابجایی، و جفتش می‌شه. بعد که همچین عالمی رو تعریف کردین، عالم‌های مربوط به عدد ۲ عالم‌های مربوط به عدد ۳ عالم‌های مربوط به عدد چهار الی آخر، که البته شما می‌تونین جورای مختلفی این کارو انجام بدین از این مبسوط‌تر باشه، مثلاً همه پرانتزگذاری‌ها رو بگیرین یا غیره که ما کاری نداریم، ولی روی همین عوالم هم می‌شه دید که عمل جمع می‌شه تعریف کرد. مثلاً اگه جابجایی باشن دوتا از این فرم‌ها رو می‌ذاری کنار هم، از عالم پشت صحنه ۲ یکی رو بر می‌داری با یک چیزی توی عالم پشت صحنه ۳ میذاریشون کنار هم می‌شه یک چیزی تو عالم پشت صحنه ۵. هم می‌شه جابجایی این کار رو کرد هم می‌شه ناجابجایی این کار رو کرد. عمل حاصل‌ضرب که روی اعداد طبیعی داریم اینم عین همون قبلی می‌شه ترجمه کرد به حاصل‌ضرب دو تا از اون نمایش‌ها، که حالا باز می‌شه جابجایی گرفت یا غیر جابجایی گرفت. مثلاً ۲ ضربدر ۳ رو مجموع دوتا دسته سه‌تایی گرفت یعنی اولی رو تعداد دسته‌ها و دومی رو تعداد چیزهای داخل اون دسته؛ ترتیب هم ترتیب قاموسی گذاشتم اگه خواستین ناجابجایی بگیرین. می‌بینیم که خیلی از ساختارهای جبری که توی اعداد طبیعی ما باهاش کار می‌کنیم توی اون عوالم پشت صحنه هم وارد میشن و این یک نگاه جدیدی به اعداد طبیعی به ما می‌ده، بنابراین نگاه جدیدی به عدد به ما میده و یک نگاه جدیدی اصلاً به کل ساختار ریاضی می‌ده؛ چون درکی که ما از ساختار داریم با کمک استعاره‌ای از مفهوم عدد درستش کردیم. خیلی از استعاره‌های پایه‌ای که برای مفهوم عدد داریم، که اینا توی کتاب لِیکاف و نونِس مطرح شده است، استعاره‌های پایه حساب، یک مقاله خلاصه‌ای هم من در رشد ریاضی نوشتم برای آشنا شدن معلم‌ها با این مفاهیم، در اون استعاره‌ها به جای عدد اگر ساختار بذاریم یک جورایی به ما می‌گن که ریاضیات مدرن از کجا اومده و با چه استعاره‌هایی جبر مدرن درست شده و ساختارهایی جبری و یا اصلاً مفهوم ساختار ریاضی. من دوست دارم که اینجا یه ذره خارج از دستور برم و راجع به مفهوم عدد که حالا نمی‌دانم آقای دکتر اکبر طباطبایی صلاح بدونن جزء این سری باشه یا جدا راجع بهش صحبت کنیم.

آرش رستگار- درباره مفهوم عدد: عرض شود که یه مقدار من فاصله‌ام رو می‌خوام از زمین دور کنم و یه ذره خیالاتی، از خیالات کمک بگیرم. عرض شود که توی قرآن یک آیه‌ای هست راجع به منازل ماه که می‌گه: قدرناه منازل لتعلموا عدد السنین و الحساب. این لتعلموا عدد السنین و الحساب یه جای دیگه هم توی قرآن اومده که به شب و روز و بنابراین به خورشید هم اشاره می‌کنه. عرض شود که، این که می‌گه عدد السنین یعنی چندین مفهوم سن وجود داره و چندین periodicity اینجا وجود داره که باید مطالعه بشه و بعد اینا روی مفهوم عدد قراره تأثیر بذارن. این‌که اینا روی مفهوم عدد چجوری تأثیر میذارن رو باید بیشتر فکر کنم اما این periodicity ها رو خیلی هاشون رو توی نجوم مطالعه کردن، محاسبه کردن، خیلی‌هاشون رو هم حساب نکرده‌اند، ولی می‌شه دید که چی‌اند. عرض شود که ماه دور زمین میچرخه هر بیست و هفت ممیز بیست و یک دهم روز، روز زمینی، یک دور دور زمین میچرخه و با محور خودش که با صفحه گذرنده از زمین و ماه، خط عمود بر اون، شش ممیز هجده دهم درجه فاصله داره، محور دوران ماه حول خودشه که اون هر بیست و نه و نیم روز زمینی حرکت دورانی ماه حول خودشه. که این فرق بین بیست و نه و نیم، و بیست و هفت و بیست و یک باعث می‌شه که ماه همیشه یک سمتش رو به زمین باشه، یک روی، نصف ماه، رو به زمین، البته اون شش درجه انحراف باعث می‌شه یه ذره از اون دور هم بعضی وقتا دیده می‌شه. خود زمینم که حرکت دورانی حول خودش داره انحرافش از خط عمود بر صفحه گذرانده از خورشید و زمین بیست و سه ممیز چهل و چهاره، که این صفحه گذرنده از خورشید و زمین که بهش صفحه خسوف و کسوف می‌گن، با اون صفحه گذرنده از ماه و زمین که بهش بگیم صفحه مدار ماه، پنج ممیز چهارده صدم درجه تفاوت داره. ما تا حالا سه تا periodicity رو صحبت کردیم؛ یکی حرکت ماه حول خودش، دور خودش محور دورانش، یکی زمین دور خودش، یکی ماه دور زمین، این می‌شه سه تا. چهارمیش این مدار ماه که بیضی هست این بیضی حول یکی از کانون‌ها دوران داره و این دوران هشت ممیز هشتاد و پنج صدم سال طول می‌کشه. پنجمین periodicity دورانی‌ست که صفحه مشترک بین دو تا صفحه‌ای که گفتم، یکی صفحه کسوف و خسوف و صفحه ماه و زمین، خط مشترکشون یه دورانی داره در خلاف جهت دوران اون بیضی که هجده ممیز شش دهم سال طول می‌کشه، این پنجمین دوران. خود محور دوران زمین حول صفحه عمود بر زمین و خورشید، صفحه خسوف و کسوف، یک دورانی داره که بیست و شش هزار سال طول می‌کشه و واسه همین حدود دو هزار سال از وقتی که زودیاک رو اینا ابداع کردن سی درجه چرخیده و زودیاک ایران عوض شده از اسد حرکت کرده. و این شش تا. هفتمی هم دوران محور دوران ماه حول خط عمود بر صفحه ماه-زمین است. این هفت تا دوران، که هر کدوم از این‌ها یک مفهوم سال می‌دن. هشتمیش این‌که خورشید و ماه و زمین توی یک خط قرار بگیرن حدود صد وهفتاد و سه ممیز سه روزه، که دو برابر این، مفهوم سال روی ماه رو می‌ده. که فصول ماه در سیصد و چهل و هفت روز اتفاق می‌افتند. پس از این هشت تا periodicity هفت‌ تا شون هیچ ربطی به خورشید نداشتن. یک periodicity زمین هم داریم که یک ساله که سیصد و شصت و پنج ممیز دویست و پنجاه و شش، نمی‌دونم چقدر، که اونم یک مفهوم سالی می‌شه نه تا. خورشید چندین periodicity داره، دوران خورشید حول صفحه عمود بر زمین و خورشیده ولی چون از مواد مذابه توی قطب هر سی و سه و نیم روز دوران داره که می‌شه ده تا. توی کمرش استوا هر بیست و پنج و نیم روز که می‌شه یازده تا. مرکز خورشید هم یکبار در هفته دوران می‌کنه سریع‌تره؛ و قبلاً در سطح هم ده برابر از این سریع‌تر بود الان کند شده، دوازده تا. یک دوران زمین حول خورشید هم که بیضیه، این بیضی حول خورشید دوران می‌کنه، سرعتشون نمی‌دونم، سیززده تا. و یه دوران خورشید حول مرکز کهکشان هم هست که می‌شه چهارده تا. بنابراین ما با چندین مفهوم سال و چندین periodicity درگیریم که حرف من اینه که اینا تأویل دارن و تا یک حدیش رو راحت می‌شه پیشرفت. مثلاً اگه ما زمین رو خود ما بگیریم، ماه رو مثل اون چیزی که مطالعه‌اش می‌کنیم بگیریم، این دوران زمین حول خودش تأویلش می‌تونه هویت ما باشه، دوران ماه حول خودش تأویلش می‌تونه هویت ماه، اون چیزی که داری مطالعه‌اش می‌کنیم. بعد دوران اون بیضی دوباره می‌تونه تأویل داشته باشه. توی عرض شود که متون قدیمی در شعر فارسی و حکمت فارسی، حکمت ایرانی، معموله که ماه رو انسان کامل می‌گیرن، خورشید رو حقیقت می‌گیرند، و اینکه یک روی ماه همیشه به سوی زمینه رو تاویل می‌کنند به اینکه انسان کامل رویش به سوی زمینه. یا یک نکته‌ای من متوجه شدم جایی ندیدم اینه که روی ماه که وایسین از کره ماه به زمین نگاه کنید همین بیست و هشت هلالی که روی ماه می بینین، ماه همون‌ها رو روی زمین می‌بینه در طول یک ماه. و اون موقعی که ماه تاریک تاریکه، زمین روشن روشنه  از منظر ماه. و اون موقعی که زمین تاریک تاریکه ماه کامله.  وقتی از منظر ماه زمین تاریک تاریکه، از منظر زمین، ماه کامل رو ما می‌بینیم. این منظر ماه، با توجه به اینکه قبلاً هم راجع بهش صحبت کرده بودم که ما منظر طیر داریم و منظر کل جبل داریم و منزل جبل داریم، بعد منظر ماه داریم و بعد یک منظر هست، منظر خورشیده که این به صحبتی که می‌خوام در آینده بکنم ربط داره. چون من سه به علاوه سه رو باید صحبت می‌کردم یه دونش جبر دروف بود، یکیش operads بود یکی higher algebras بود، اینا سه تا روش جبر انجام دادن بودن که می‌خواستم تشویق کنم، اون سه روشی که می‌خوام نقد کنم، تحقیقات در جبر جابجایی و جبر ناجابجایی و سومیش هم در نظریه گروه‌هاست. که اونجا من به منظر خورشید توی توصیف جبر ناجابجایی احتیاج دارم. چون یه نگاه خوبی اونجا هست که این منظر اونجا معنی پیدا می‌کنه. پس من سه تا منظر تشویق تحقیقات در جبر رو تموم کردم، نوبت می‌رسه به سه تا منظر نقد.

آرش رستگار- نقد تحفیفات در جبر جابجایی: بسیار خب حالا من می‌خوام از سه به علاوه سه، سه دومش رو که یعنی اون قسمت انتقادی از روش انجام دادن جبر هست رو راجع بهش صحبت کنم؛ یعنی اون قسمت‌هایی که تشویق بود سه تا رو گفتم که higher algebras بود و operad بود و نمی‌دونم فرمول‌بندی دروف بود، بعد حالا می‌خوام سه تای دوم رو که جبر جابجایی باشه و جبر ناجابجایی باشه و نظریه نمایش گروه‌ها و گروه‌ها باشه که اعتراضاتی که بهشون دارم رو بگم. اولاً که حالا این صحبت راجع به نقد روش انجام دادن جبر جابجاییه ولی یک انتقاد کلی که من به این روش دارم که اینا خیلی اصل موضوعه‌ای کار می‌کند، خیلی p آنگاه q ای کار می‌کنند. فکر می‌کنن ریاضی انجام دادن یه بازی اثباته که شما چند تا چیز و چند تا اصل موضوعه رو به کار ببرین ببینید چی بدست میارین. و خیلی از اشکال‌هایی که به جبر وارده از همین‌جاست، چون جبر احتیاج به insight داره و این روش insight نمی‌ده. کسایی هستن، مثل دکتر کرم‌زاده، می‌گن که شما باید p آنگاه q نباشه، p اگر و فقط اگر q کنید قضایا رو تا عمیق‌تر بفهمید. این فایده نداره، اون insight رو نمی‌ده. باید ارتباط جبر رو با شاخه‌های دیگه ما بفهمیم؛ و به خصوص تو جبر جابجایی که خیلی ممکنه. مثلاً همه این چیز جای توی جبر جابجایی با هندسه جبری ربط دارند؛ نمی‌شه کسی هندسه جبری بلد نباشه، جبر جابه‌جایی انجام بده به همین روش اصل موضوعی. و شما جوایز جبر هم که در سطح بالایی هستند نگاه کنین مثل جایزه کوُل، که در نظریه اعداد و در جبر داده می‌شه، می‌بینین که اینا همش تحقیقات برجسته تحقیقات بین رشته‌ای اند که ما از یه جا insight می‌گیریم یه جای دیگه توی جبر اینا رو پیاده می‌کنیم. و جبردان‌های بزرگم می‌بینین که همچین آدمایی بودن. اون آدمایی که تأثیرگذار بودن مثل هایمن‌بس، مثل کوییلن و دیگران، اینا کسایی بودن که سرچشمه‌ها را از شاخه‌های دیگه وارد جبر می‌کردن یا وارد نظر اعداد می‌کردن. یا اصلاً نظریه جبری اعداد شکلش همینجوریه که همه‌اش از سرچشمه‌های که توی شاخه‌های دیگه وجود دارن سیراب می‌شه. اصلاً جنس این شاخه اینطوریه. بعد شما اینجوری انجام ندین چجوری انجام بدین؟ من می‌گم مثل کتاب اقلیدس که بگه قضیه اثبات، بنا بر قضیه فلان، قضیه بهمان رو ثابت می‌کنیم، مفهوم تعریف می‌کنه و ...، اینکه شما ریاضی رو این بدونین نه اینکه این روش اقلیدوس رو لباس ریاضی بدونین، اصل ریاضیات بدونین، باعث می‌شه ریاضیات بی‌مایه تولید بشه. و خیلی از تحقیقات جبر جابجایی امروز در دنیا بی‌مایه است و خیلی از اینا هم، در ایران بیشتر، از همین نوع ریاضیات و ریاضیات انجام دادن پیروی کنن. و حالا این تفکر اصل موضوع یک جاهایی هم هستش که من توی قسمت ناجابجایی صحبت می‌کنم، که مفید هم هست، contribution  هایی داره، تأثیرات مثبتی داره، که اون جایگاهش رو من عرض می‌کنم. کسانی هم که متأسفانه تو جامعه ریاضی ما جبر جابجایی‌شون خیلی خوبه و شاخه‌های همسایه رو خوب بلدن، توی جامعه جبر جابجایی، بین اون کلونی اصلی، پذیرفته نمی‌شن. ترد میشن. جاب بهشون نمیدن. بهشون احترام نمیذارن. تحقیقاتشون رو برجسته نمی‌کند. چرا که خب اگه اونا بولد بشن، این تحقیقات بلد بشن، کارهای خودشون بی‌ارزش به نظر می‌رسه. حالا اینا ابعاد انسانیه، خیلی به نوع ریاضی انجام دادن مربوط نمی‌شه. ولی بازم یه چیزی که من از دکتر اکبر طباطبایی یاد گرفتم رو اینجا خوبه بگم که هیلبرت بود که این روش جبر جابجایی رو نو کرد و تازه کرد و احیا کرد؛ قبلاً invariant theory که اواخر قرن نوزدهم انجام می‌دادن استاد هیلبرت و اینا، این‌ها میومدن هر حلقه‌ای رو به‌صورت یک quotient از حلقه چند‌جمله‌ای‌ها در نظر می‌گرفتند، و با generator هاش بازی می‌کردند. و هیلبرت بود که گفت نه این روش درست انجام دادن ریاضی نیست و این روش جدید جبر انجام دادن رو بنیان‌گذاری کرد و باهاش قضیه اساسی invariant theory را هم ثابت کرد و یک مکتبی درست کرد که بعداً امی نوتر و دیگران اومدن بهش پیوستن و بعد فلسفه فرمالیسم رو به وجود آورد که فلسفه فرمالیسم رو در مقالات فلسفیش نتونست خوب پیاده کنه، اون اونجوری گفت که انگار که فرمالیسم یعنی بازی با نماد، در صورتی که اینجوری نیست. فرمالیسم یعنی درک یه عالم بالاتری از عالم ساختارها، یک نگاه کل‌نگرانه و سرتاسری‌تری از عالم ساختارها. یعنی نگاه عالم صورت‌ای نگاه عالم رسم‌ای و نگاه فرمی به ساختار، یا نگاه رسم در برابر اسم، که اسم باشه ساختار. این نگاه رو معرفی کرد که اونطوری که من یاد گرفتم این خیلی نزدیکه اتفاقاً به فرمول بندی براور و براور هم یه ذره از این تازه پیشرفته‌تره، از آن هیلبرت یه ذره پررنگ‌تر همین حرف رو می‌زنه و اختلافاتشان اختلافات عمیقی نیست، بیشتر بقیه ریاضی‌دان هستند که اینا رو نمیفهمن و مطالعه عمیق‌تر نشون داد که مفهوم صورت ارسطو هم همین مفهوم عمیق بود ولی پیروانش نفهمیدن و دلیلش اینه که خب وقتی یه عالمی رو کسی تجربه چشیدنش رو نداره جملات براش اون معنی که باید رو نمی‌دن دیگه فکر می‌کنه یک معنی دیگه می‌دن. برای کسی مثل فارابی است که ارسطو همون افلاطون است. کسی که زیر عالم اسماء می‌خواد فکر کنه متوجه یکسان بودن اون چیزی که اینا دارن بیان می‌کنند نمی‌تونه بشه. و همون‌طور که دکتر اکبر طباطبایی تذکر دادن ما به ریاضیات هیلبرت که نگاه می‌کنیم می‌بینیم سرشار از فرمه، سرشار از درک عمیقی از صورته. بنابراین من می‌خوام بگم که هیلبرت بله و این روش‌های امروزی جبر جابجایی خیر. یعنی ما آدمای تازه کار و نپخته و ناآگاهی از ریشه‌های ریاضیات و ریشه‌های علم جبر در شاخه‌های دیگر ریاضیات داریم که هی میان مفهوم تعریف می‌کنند هی قضیه ثابت می‌کند می‌گن ما فلان قضیه رو به فلان حالت کلی‌تر تعمیم دادیم حالا بعد میری می‌بینی تعمیم رو نه اصلا نمی‌شه استفادش کرد، نه مهمه، نه مفاهیمش اصلاً به درد می‌خورن، نه اصلاً به طور طبیعی پیدا میشن، نه هیچ‌وقت اون مفاهیم و فرضیات قضیه اصلاً پیش نمیان تو زندگی واقعی یک ریاضی‌دان که اصلاً از اون تعمیم اون قضیه استفاده کنه. بعدمی‌گی حالا ببینم شاید تعبیر فلسفی داشته باشه، تأویل عمیقی داشته باشه. بعد می‌بینی نه واقعاً تهی است. این روش جبر انجام دادن احتیاج داره که یک آدمی که ویژن داشته باشه، عمیق بفهمه ریاضیات به کدوم سمت باید بره، نظر بده. و آدمایی که حالا در جبر جابجایی اند ممکنه توی دنیا خیلی معروف هم باشند مثل مثلاً هرزوگ و نمی‌دونم اون school جبر جابجایی اون کشورهای اسکاندیناوی و اینا، ولی اینا لزوماً، می‌گم لزوماً، ریاضیات عمیقی نیستند. اینجوری نیست آدم بگه خب من می‌رم از اون مکتب پیروی می‌کنم و ما هم بشیم یه چیزی. این نقدی است که به این نوع ریاضی جبر جابجایی وارد می‌کنم و این مهمه چون ترکیبیات و جبر جابجایی و منطق فازی سه تا رشته ریاضی اند که در ایران کلونی دارند یعنی عده‌ای با هم کار کند، به مقالات هم رفرنس می‌دن، از کارهای هم آگاه اند، به کار هم ارجاع می‌دهد؛ برخلاف شاخ‌های دیگه. و مهم است که همچین چیزی رشد سالمی داشته باشه، عمیق رشد کنه، به مسائلی که مهم‌اند بپردازه، تا استعدادهای ما،  استعدادهای دانشجوهای ما، اساتید ما جایی که درسته خرج بشه، زحماتشون اون زمینی که مناسبه درش اون حَب رو بکاره، که بعد باغ خوبی بیرون بیاد. و الان اینجوری نیست. در جامعه جبر جابجایی ما رهبران درست و حسابی نداریم. این یک مسئله ریاضیه، مسئله انسانی نیست. آدمای خیلی خوبی اند ریاضیدان‌ها. خیلی سالم‌اند، مهربونن، ولی هدایت یک شاخه فرق داره با مهارت‌های انسانی. این‌ها یک نگاه کل‌نگر به ریاضیات احتیاج دارن.

آرش رستگار- درباره مهارت تجرید: یک سؤالی میپرسن جناب نادری که بعضی از ریاضی‌دان‌ها، این مقاله فریمن دایسون هست Birds and Frogs، می‌گه بعضی‌ها مثل قورباغه اند، گل رو حفر می‌کنند اون زیر رو در میارن؛ بعضی‌ها مثل پرنده اند، از بالا یه چیزایی می‌بینن. و بعد اشاره می‌کنن به یک قسمتی از گفت‌وگوهای قبلی، که گفته می‌شه در همین سری خودمون، که بعضی اون قدر بالا می‌رن که دیگه می‌رن بالای ابرها و دیگه زمین رو نمیبینن و ارتباطشون رو با واقعیت دیگه از دست می‌دن. و اون وقت ریاضیات مجردی انجام می‌دن که لزوماً ریاضیات مفیدی نیست. و آیا نتیجه اینه که این کار تجرید و مجرد فکر کردن با فقط دست یک عده خاص باشه که تواناییش رو دارند؟ آیا اینجوری فکر کردن کار خوبیه یا خیر؟ عرض شود که اون دوتا مفهوم در اون مثالی که شما بالا میرین کل‌نگریه؛ درسته که کسایی که مجرد فکر می‌کنند کل‌نگرن، ولی کسایی که توی جبر جابجایی اند خیلیاشون کلامی جزءنگرن ولی گسسته، که جبر جابجایی انجام می‌دن. اصلاً ایراد همینه که نگاه کلی به ریاضیات ندارند. ولی این هم که از یک جایی مجردتر شدن هم کار سختیه و به آدمایی که توانایی علمی و اون گستره علمی دانش رو دارن نیاز داره نکته درستی هست، ولی اون جبر جابجایی‌دان‌هایی که مورد نظر من هست اون آدمایی نیستن که اون حکمتی که شما می‌گین بهش اشاره می‌کنه. مثلاً می‌خواد بگه که یه مدتی بعد از فوت گروتندیک اینجوری بود که اون ریاضیات گروتندیک رو کسی نمی‌تونست به خوبی خودش انجام بده. چون کسی اون ویژن لازم رو نداشت. همین الان هم بعضی‌ها هنوز فکر می‌کنن بعد از گروتندیک کسی نتونسته اون بلند پروازی که اون داشت رو بهش دسترسی پیدا کنه. هر چند که من بعید می‌دونم، یعنی یک عده‌ای، نسلی از ریاضیدان‌ها، رشد کردن که الان در دهه چهل سالگی‌شون و اینا هستن که خیلی عمیق پرواز کردن، کارهای گروتندیک هم ادامه دادن؛ و نمی‌دونم حالا بگیم پیش‌قراول یا کسایی که در خط مقدم میجنگن، آدم‌هایی مثل همین کسانی که دارند higher algebras انجام می‌دن که مهم‌تر از همه این استاد انستیتو است، که ترم پیش هم شروع کردیم کتابش رو درس بدم، جیکوب لری، و عده زیادی هستند و school های زیادی هم هستند که آدمای موفق هم توشون بسیار زیاده. همین اخیراً  Gaitsgoryلنگ‌لندز پروگرام حالت توابع روی C رو، Geometric Langlands program رو achievment بزرگی داشت. این حرف هم پس درسته که بله از یک حدی مجردتر فکر کردن احتیاج به آشنایی با پهنه وسیعی از ریاضیات داره؛ آدم باید استعدادش هم داشته باشه، خودش رو هم برای این کار تربیت کرده باشه سال‌ها، تا بتونه درست در این مسیر حرکت کنه. بایدها و نبایدهای شناختی و اجتماعی و ریاضی رو بلد باشه. چون شما باید بدونین کجاها پاتون محکمه، کجاها زیر پاتون محکم نیست، چه چیزهایی رو جامعه ریاضی حاضره بپذیره دنبال کنه، چه چیزهایی رو حاضر نیست، یا مانند این. چون مثلا بعضی از فرمول‌بندی‌ها رو مثلا میان یه فرمول بندی از higher categories می‌دن، بعد مردم میترسن follow کنند نکنند، مقاله بنویسند ننویسند، ممکنه جامعه ریاضی نپذیره، چون چندین فرمول‌بندی suggest شده. بنابراین اینا رو باید یک نفر خوب بدونه که ابعادش چیه که بخواد وارد این جنگ بشه، وارد این حیطه بشه.

آرش رستگار- نقد تحقیقات در جبر ناجابجایی: خیلی خب در نقد روشی که جبر ناجابجایی ما انجام می‌دیم، یکی این‌که همون نقدی که بر جبر جابجایی گفتم اینجا هم وارده، مثلاً ما توی C*-algebra یک عالمه متخصص داریم ولی خب این‌ها باید همه الن کن رو بلد باشن. الان باید این همه متخصص C*-algebra داریم، ریاضیات الن کن باید در ایران شناخته شده باشه؛ ولی نه فقط شناخته شده نیست، بلکه می‌گن نه اون خوب بلد نبود انجام بده، ما خوب بلدیم ریاضی انجام بدیم. بدون اینکه کارهای الن کن رو فهمیده باشن. پس یک نقد اینه که از سرچشمه‌ها فاصله گرفته. نقد دوم اینکه جبرهای ناجابجایی، اصلاً skew field ها قابل deform کردن اند می‌تونن حرکت پیوسته داشته باشن؛ چیزی که می‌تونه حرکت کنه، که میدان نمی‌تونه چون solid است، ولی وقتی اجازه دادین ناجابجایی باشه می‌شه دیفورمش کرد، این‌ها باید in families مطالعه بشن، نباید دونه دونه مطالعه بشن. خب ما از مثلا هامیلتون به بعد یاد گرفتیم، که انیشتین به ما یاد داده بود و ما ریاضی‌دان‌ها نفهمیده بودیم، که ما باید متریک رو دیفورم کنیم، فضای هندسی رو باید دیفورم کنیم؛ که منجر به اثبات حدس پوانکاره شد، همین مسئله در جبر ناجابجایی هم وارده. خیلی‌ها میان جبر ناجابجایی رو دونه دونه، مثل همون آدم‌های جبر جابجایی که اینکار رو می‌کنن، دونه دونه مطالعه می‌کنند، نه in families. و چیزایی که خانوادن، ما از گروتندیک یاد گرفتیم باید in families مطالعه بشن؛ چون اصلاً مفاهیمش باید in families تعریف بشن، relative باید تعریف بشن. این دوتا نقد، که این نقد رو راجع به اینکه باید این‌ها رو دیفورم کنیم و بنابراین موجودات هندسی اند، جبرهای ناجابجایی موجودات جبری نیستن موجودات هندسی اند چون می‌شه دیفورم‌شون کرد رو من توی گروه‌ها هم تکرار می‌کنم، بنابرین اینجا طولانی نمی‌کنم. منتهی یک قسمت سومی هست در این نقد جبر ناجابجایی که این در واقع تعریفه و نقد نیست، و این رو من از دکتر رضا فلاح مقدم یاد گرفته‌ام و این به خاطر تجربیاتیه که با استادشون دکتر مهدوی هزاوه‌ای داشتن که برای من این‌طور تعریف کردن: ببینین تجربه ریاضی‌ای که وایلز تعریف می‌کرد بعد از اثباتش، تجربی ریاضیش رو تشبیه می‌کرد به یه آدمی که توی یک اتاق تاریکه و می‌خواد ببینه چی هستش و می‌گرده با انگشت‌هاش نمی‌دونم پیانو رو پیدا می‌کنه، اتاق خواب و تخت خواب رو پیدا می‌کنه، پاش محکم می‌خوره به یه صندلی درد می‌گیره، همین‌جور کورمال کورمال، آخر کلید چراغ برق رو پیدا می‌کنه و روشن می‌کنه و همه چیز معلوم می‌شه. این تجربه رو من توی یک مقاله‌ای بعدها مقایسه کردم با تجربه‌ای که خانم میرزاخانی می‌گه که انگار من توی یک جنگل ام، گم شدم، نمی‌دونم از کدوم ور از جنگل بیام بیرون، از تپه می‌رم بالا که یک منظری ببینم، خورشید رو ببینم، و از اون بالا ساختار کوه‌ها و طبیعت رو که می‌بینم می‌فهمم با چه مسیری باید کدوم سمتی برم تا بتونم از جنگل بیام بیرون. این‌ها رو من توی یک مقاله‌ای مقایسه کردم که خلاصش اینه که می‌گه اون آدمی که وایلز باشه، که ریاضیاتش کلامیه، هم اون اتاقه و هم همه اشیاء توش ساخته دست انسان اند؛ و اون کسی که تصویریه، کل‌نگره، هم اون جنگله و هم همه چیزایی که داره دنبالش می‌گرده ساخته دست انسان نیستند، اون داره کشف می‌کنه. اون یکی خلق است این‌ها همه‌اش کشف است. بعد یه تجربه سومی بود که دکتر آراسته و خانم‌شون در خیام خیّام بیان کردن؛ دکتر آراسته اول گفت مثل کوهنوردیه که شما بالای کوه می‌رین از اون بالا می‌خواین ببینین، و شما یک دانشجو لزوماً این همه راه بیاد با شما تا کوه بالا و برسه اون بالا بگه چی بود حالا، همین رو می‌خواستی بمون نشون بدی؟! به زحمتش ممکن نیرزه. یا بعد خانمش گفت اصلاً کوه شما رو باز دستتون به خاک می‌رسه، ما انگار که در هواپیما هستیم از اون بالا همه چیز رو می‌بینیم، هیچ دستمون هم به چیزی نمی‌رسه. خانمشون دکتر حبیبی می‌گفت من توی یک سمیناری اخیراً توی زنجان شرکت کردم، آنالیزدان‌ها صحبت می‌کردن، جبردان‌های صحبت می‌کردن، گفتم خوش به حالشون، این یکی مثل ساحله، اون یکی مثل دریاست، اون یکی مثل جنگله، شما به یه چیزی می‌تونین دست بزنین؛ هندسه جبری هیچی دستتون نمی‌رسه، همش باید از اون بالا کلی فکر کنین. بعد من از دکتر میثم نصیری شنیدم که عبارت‌های مشابه این رو کوچر بیرکار گفته که ریاضی انجام دادن برای من مثل یک پرنده‌ایه که داره از بالا یه شهر رو نگاه می‌کنه. که البته این دوتا جالبه که به فرقش توجه کنید، اون هندسه جبری دان هست و داره به شهر نگاه می‌کنه، به ساخته‌های دست بشر، ولی پرنده است یعنی ساخته خداوند. اینی که آقای آراسته و خانمشون می‌گن خودشون سوار هواپیما اند که ساخت بشره ولی از اون بالا دارن طبیعت رو نگاه می‌کنن. این‌ها باز دوتا چیزه. ولی من این‌ها رو گفتم مقدمه، که اون ورژن دکتر فلاح رو بگم؛ که می‌گه ما که ریاضی انجام می‌دیم در جبر ناجابجایی، انگار که یه آسمون عظیم سیاهیه، و شما دو سه تا ستاره اون وسط دارین و حالا باید راهتون رو پیدا کنین. گفت اصلا ما همش داریم ثابت کنیم چه چیزایی وجود ندارن. اگه یکی از ما بپرسه که برای حرفایی که گفتی یه مثال بزن، انگار عصبانی می‌شیم می‌خواییم سرمون رو بکوبیم به دیوار! چون نمی‌تونیم مثال بزنیم. چون همش حرف‌مون اینه که اون دو سه تا ستاره تنها چیزاییه که می‌شه با این شرایط پیداش کرد. بنابراین این منظر که این‌قدر بلنده، نتیجه همون تفکر مجردیه که من بهش اعتراض کردم. بنابراین نمی‌شه بگیم که نه اصلاً اون نباشه. بگیم اقلیدس اصلاً نباشه. اقلیدوس دو هزار سال ریاضیات رو مدیریت کرده، نمی‌شه گفت اقلیدس نباشه؛ می‌شه گفتش ولی به اقلیدوسی‌ها که شما یه ذره جا رو باز کنین، یه دکون دیگه هم اجازه بدین کنارتون وجود داشته باشه. قرار نیست همه پول‌ها توی جیب شما بره، همه مشتری‌ها بیان از شما خرید کنن. اون‌های دیگه هم آدم اند. عرض شود که نتیجه‌گیری: ما یک منظر کوه داریم، یک منظر «طیر» داریم، که اگه «علی کل جبل» «طیر»ها رو بذارین، منظر همه کوه‌ها رو داشته باشین، ازش منظر «طیر» بیرون میاد؛ بلکه منظر چند «طیر» بیرون میاد و منظر طیر یگانه نیست. و بعد منظر قمر است؛ شما از ماه بیایین کل زمین رو ببینین. که اونم باز یه نکاتی داره، که شما از منظر قمر، زمین می‌چرخه همه زمین و همه جاش رو می‌تونین ببینین؛ ولی اون چیزی که مطالعه می‌کنید همون کل ریاضیاته، که کل زمین باشه. و بعد یه منظره خورشید هم هست که دیگه اون زمین براش یه نقطه کوچیک سفیده که اونم نورش رو از خودش گرفته. و مطالعه این منظر خورشید، داره کل آسمان‌ها رو نگاه می‌کنه. که همان منظریه که دکتر فلاح مقدم گفت. اینم بگم که اون نگاه خیلی از دور و عمیق و مجرد، اگه درست انجام بشه چیز خیلی با ارزشی هم هست؛ مشکل اینه که درست انجام بشه. همه می‌خوان بشن گروتندیک، خوب نمی‌شه، مگه چندتا گروتندیک داریم، مثلاً چندتا شاگرد اول داریم. من یادمه کلاس المپیاد فیزیک بودیم، یک استاد دانشگاه شهید بهشتی بود، اسمشون یادم نیست، به ما فیزیک درس می‌داد حتی یادم نیست مکانیک درس می‌دادند گرما درس می‌دادند چی درس می‌دادند، ما یک کلاس مثلاً پنجاه نفره بودیم، پنجاه و پنج نفره بودیم، قرار بود یک تیم نمی‌دونم شش نفر از بین ما انتخاب بشه و استاد ما می‌گفت همیشه که من برای همه شما آرزو می‌کنم که همتون جزو اون تیم شش نفره باشین. خب جا نیست، نمی‌شه مثلاً یک قومی همه‌شون رهبر باشند. ریاضی‌دان‌ها همه‌شون بشن گروتندیک. نه، گروتندیک در یک رقابتی بین چندتا نصف گروتندیک، گروتندیک شده. اون نصف گروتندیک‌ها در یک رقابتی بین چند تا ربع گروتندیک، نصف گروتندیک شدن. این‌هایی که فیلدز می‌گیرن، چندتا کله گنده دورشون اند که این‌ها با هم کار کردن، در رقابت با اون‌ها این‌ها بالا اومدن. مثلاً خانم میرزاخانی چند تا همکار داره که همه اینا خب همون ریاضی رو انجام دادند؛ در رقابت با اون‌ها این شخص برجسته شده. مثلاً آقای دکتر امیرمحمدی هست، نمی‌دونم آقای دکتر کسری رفیع هست همون ریاضیات رو کار می‌کنه. حالا الکس اسکین هم هست. و افراد دیگه‌ای که این‌ها رقابت می‌کند یکی‌شون میاد بالاتر. توی فیلدزهای دیگه هم اینطوریه. کسی که تنها باشه، یا تأثیرگذار نتونه باشه اون ریاضیات، نمیان بهش فیلدز بدن؛ چون فیلدز دادن یعنی باید یک عده‌ای یا یک گروهی رو این‌ها promote کنن و تشویق کنن. این از نقد جبر ناجابجایی، که البته همه‌اش شد تشویق که!

آرش رستگار- جبر جابجایی و ناجابجایی در برابر فیزیک کلاسیک و کوانتوم:

عرض شود که آقای نادری میپرسن که این مسئله تقابل جبر جابجایی و جبر ناجابجایی ما عینش رو توی فیزیک کلاسیک در برابر کوانتوم باهاش درگیریم؛ که اونجا کوانتوم، جبر رو جابجایی می‌کنه و اگه شما اون h رو به سمت صفر میل بدین، جبرتون جابجایی می‌شه و با همین مسئله مفاهیمی که در جبر جابجایی و ناجابجایی هست شما سروکار دارین. اصلاً به همین دلیل هندسه ناجابجایی‌اش رو مثلاً الن کن میاد به فیزیک ربط می‌ده. یا می‌بینید که مثلاً یه آدمی مثل کانسیوویچ میاد deformation quantization اش رو انجام می‌ده، که از همین ایده‌های فیزیک کوانتوم سرچشمه می‌گیره، که بعد باهاش می‌تونه مثلاً یک قضیه مهمی رو ثابت کنه که بخاطرش فیلدز گرفت و بعد مریم میرزاخانی هم به خاطر اثبات دوم و بهترش شهرت پیدا کرد. چرا اتفاقاً این یه جور خوب انجام دادن جبر جابجایی و ناجابجاییه، مثال خوبی زدین، و این تقابل خیلی روشنگر بوده در ریاضیات؛ به چیزای خوبی منجر شده. بنابراین اون انتقادهایی که من داشتم به این جور جبر ناجابجایی مربوط نمی‌شه. ولی خب هستن، ولی کم هستن، ریاضی‌دانایی که کارشون جبر ناجابجاییه ولی ریاضی-فیزیک کار می‌کنند. معمولاً اون کسایی که ریاضی-فیزیک کار می‌کنن، خب هم جبر کار می‌کنند هم چیزهای دیگه‌ای که به فیزیک مربوط می‌شه کار می‌کنند، مثلاً از انواع ریاضیاتی که از اینجا اومدن وارد ریاضیات شدن سرچشمه‌هاشون اینجا بود، مثلاً vertex operator algebras است که خیلی آدم‌های قوی‌ای هم داشتیم، که حتی به فیلدز هم رسیدن مثل مثلاً بورچرد و این‌ها که خیلی چیزهای مختلفی هم کار می‌کردن. جبری که به فیزیک مربوط باشه، و هر شاخه ریاضی، هندسه ناجابجایی که به فیزیک مربوط باشه، نمی‌دونم deformation متریک که به فیزیک مربوط باشه، هندسه‌ای که به فیزیک مربوط باشه مثل اون کارهای Ricci flow و Mean curvature flow و اینا، این‌ها همه ریاضیات ارزشمندی اند؛ چون طبیعت سرشاره از حقیقت.

آرش رستگار- نقد تحقیقات درنظریه گروه‌ها: عرض شود که همین انتقادات در نظریه گروه‌ها، ببینین این نگاهی که ریاضیات یعنی اثبات گزاره‌ها و تفکر منطقی و همه ارزش ریاضی به اثبات‌هاش و قضیه‌هایی که ثابت کنیم خلاصه می‌شه، توی نظریه گروه‌ها دیگه خیلی پررنگ می‌شه. یعنی می‌بینید بعضی وقت‌ها یک شرایطی میذارن این مثلاً finite group theorist ها و میان شروع می‌کنن به رده‌بندی گروه‌هایی که توی اون شرایط صدق می‌کند، که اصلاً تو دکون هیچ بقالی پیدا نمی‌شه! هیچ جا شما اون شرایط رو ندارین. می‌گه خب من این‌ها رو می‌تونم رده بندی کنم؛ یا مثلاً فلان مثال جالب این‌ها داشته، من می‌خوام رده‌بندی‌اش کنم. یعنی، من یادم نیست، یکی از دانشجوهام تعریف می‌کرد از یکی از کلاس‌های درسش، می‌گفت استاد ما اصلاً مخصوصاً یکی ازش پرسید که فلان شرط رو چرا گذاشتی که بررسی کنی؟ اون هم جواب داده بود که ریاضی همینه دیگه، ما یک فرضی می‌کنیم ببینیم حالا چی می‌شه، چه نتایجی می‌ده. بنابرین اصلاً تصورشون راجع به ریاضیات اینه. خب ما group theorist های بزرگ هم داریم، مثل جان کانوی همه ریاضیات رو روش سواره، نمی‌دونم مثال خیلی زیاد می‌شه زد، من الان مثلاً ده تا نام ببرم قشنگ معلوم می‌شه کدوم شاخه‌های group theory رو من بلد نیستم، چقدر با سوادم چقدر بی‌سوادم. برای همین یک مثال نمی‌زنم که شما فکر کنید کاملاً بی‌سوادم. یه نکته دیگه هم یاد‌آوری کردن آقای موسوی که ما در صحبت ترکیبییات گفته بودیم که finite group theory و profinite groups این‌ها اصلاً جزو ترکیبیات باید محسوب بشن نه جزو جبر. و من الان یه ذره بیشتر جلو می‌رم، اصلاً discrete groups هم که مربوط به تقارن‌های discrete اند یا اصلاً تقارن‌های discrete objects اند، این‌ها باید جزو ترکیبیات باشن لزوماً اینجور نیست ترکیبیات‌دان‌ها موجودات متناهی رو بررسی کند؛ که توی قسمت ترکیبیات من راجع‌ به شلاح و ریاضیات شلاح و این‌که چقدر کسانی که نظریه مجموعه‌ها کار می‌کند شبیه اند به کسانی که ترکیبیات کار می‌کنند، و شلاح هم چقدر مقاله ترکیبیات داره و ابعاد شناختی‌اش و این‌ها، قبلاً دیگه صحبت کردم و اینجا واردش نمی‌شم.  مثلاً گروه گالوا خب یک profinite group است و group theorist ها به این سادگی نمی‌تونن مطالعه‌اش کنند. باید یک مقدار زیادی نظر اعداد بدونن، یا یک مقدار زیادی هندسه جبری بدونن. اون نگاهی که معمولاً در group theory حاکمه، اینجا حاکم نیست. حالا حتی کسانی هم هستن اصلاً همین جوری هم که من می‌گم بده group theory انجام می‌دن ولی group theory خوب انجام می‌دن، چون باسواد اند، چون عمیق اند، چون دید کل‌نگرانه دارند. آدم‌هایی مثل آیزکس که استاد دکتر رضا شهریاری است که پسر پرویز شهریاری معروف است. این یک نکته. نکته دوم اینکه گروه‌ها هم چون موجودات ناجابجایی اند موجودات هندسی اند. اصلاً ما گروه‌ها رو به عنوان گروه تقارن می‌شناسیم، گروه تقارن چی؟ و ما از هندسه شروع کردیم پس این‌ها موجودات هندسی اند. پس این‌ها رو باید بشه deform کرد. اگر هم نمی‌تونین deform کنین، برین تو فرمالیسم ناجابجایی، برین تو quantum groups، و این‌ها رو deform می‌کنین. این‌ها باید این‌طوری مطالعه بشن؛ نمی‌شه کسی موجودات هندسی رو با روش‌های purely algebraic مطالعه کنه و گروه‌ها موجودات purely algebraic نیستند. یعنی، بذارید اینجوری بگم، متخصصان نظریه گروه‌ها غالباً خودشون رو جبردان می‌دونن ولی این شاخه اصلاً خالصاً مخلصاً جزو جبر حساب نمی‌شه، ریشه‌هاش جاهای دیگه است. خب خیلی شاخه‌های دیگه جبر  هم همین‌جوری اند و آدم‌ها رو به‌خاطر اینکه به ریشه‌هاش وصل نمیشن من تقبیح می‌کنم. این دوتا، سومی اینکه فرض کنین یه نفری اومد یه ایده‌ای رو مطرح کرد، یه مفهومی آورد که این مفهوم مهمه؛ مثلاً super manifolds توی فیزیک مهم می‌شه، شما super geometry رو با این ورژن super mathematics می‌تونین فرمول بندی کنید. خیلی مهمه، بدون سوپر نمی‌شه فرمول بندی کرد. پس ریاضیات سوپر بله مهمه. پس super representaions of super Lie groups بله مهمه، ولی دلیل نمی‌شه که شما برین الان همه گروه‌ها رو مثلاً گروه‌های متناهی هر چی دستتون اومد بیایین راجع به super representaion هاش فکر کنین. مثلاً بگین آقا یک چیز جدیدی اومده بهش می‌گن super representaion، یک فضاهای برداری هست بهش می‌گن super vector space،  بیایین آقا بشتابید الان مد شده راجع به مثلاً super representaion of finite groups مقاله بنویسیم. و ایران group theory اش اینطوریه. یهویی مد می‌شه به یه چیزایی که هیچ آدم باتجربه‌ای روش دست تأیید نمیذاره اشتغال پیدا می‌کنه. و چون این‌ها با هم ارتباط دارن، گروه اند، از کارهای هم مطلع اند، به هم رفرنس می‌دن، تحقیقات هم رو ادامه می‌دن، یه نفر دو نفر نیست که آدم بگه نه خب حالا اجازه بدین هر کار دوست داره بکنه. مثلا C*-Algebra کار های ما خیلی زیادن، group theorist های ما خیلی زیادن. آره یکی دوتا استاد بودن، چندین شاگرد داشتن الان یه عالمه شاگردها دارن این ریاضی رو انجام می‌دن با هم ارتباط دارن. عین این توی آنالیز تابعیه؛ یکی دوتا استاد آنالیز تابعی بزرگ داشتیم، این‌ها یه عالمه شاگرد تربیت کردن، این‌ها دیگه الان کلونی اند. حالا که کلونی اند مهمه درست ریاضی انجام بدن. به خاطر چی؟ چون resource های ما رو مصرف می‌کند؛ و مهم‌ترین resource ها گرنت‌های ما نیستن، دانشگاه‌های ما نیستن، پوزیشن‌های ما نیستن، آدم‌های ما هستن. محقق‌های ما هستن. و باید یجوری ریاضی انجام بدن که این‌ها شناخت‌شون رشد کنه، کمال پیدا کنه، به اون قله‌های شناختی‌ای که ریاضیات می‌تونه ریاضی‌دان رو تربیت کنه برسند. ولی اصلاً راجع به همچین چیزهایی که گفتم و کلماتی که گفتم، نه کسی از این کلمات چیزی شنیده، نه اصلاً قائله به اینکه ریاضی همچین توانایی‌ای داره، و نه اصلاً نگاه می‌کنه ببینه تو دنیا چی‌کار می‌کنن. و این باعث شده این کلونی‌هایی که هست جهان‌گیر میشن؛ یعنی یهویی شما می‌بینید یک جور ترکیبیاتی هست توی همه جهان سوم زیاد هست، و بعضی وقت‌ها کم کم توی دانشگا‌های خوب هم ممکنه یکی‌شون برسه. مثلاً ما یک جور جبری هست، جبر جابجایی‌ای هست در انگلیس مخصوص دانشجو دکتری‌های خارجی؛ که اینا پول بیارن اینجوری حالا دکتری بگیرن برن. خوب استادهای ما خیلی‌هاشون اینجوری دکتری گرفتن، خودشون هم خبر نداشتن. نه از دنیا خبر داشتن، ولی خیلی هم باهوش بودن خیلی هم توانا بودن اومدن توی این شاخه درس خوندن، خب ما به این آدم‌ها نیاز داشتیم این‌ها بهترین آدم‌هامون بودن، مهمه که این‌ها درست راهنمایی بشن. بنابراین مهمه ما اعتراض کنیم که بگیم ریاضیات رو باید درست انجام داد و اگر کسی هم مخالفه می‌گه آقا شما اشتباه می‌کنی، من به این دلیل به این دلیل به این دلیل با شما مخالفم، و ما اینجوری اینجوری اینجوری ریاضی انجام میدیم و ما درست ریاضی انجام می‌دیم، اصلاً همچین دیالوگی نیست. اصلاً می‌گن کسی با کسی حرف نزنه راجع به ریاضیات خوب و ریاضیات بد. کی می‌تونه بگه چه ریاضی‌ای خوبه چه ریاضی‌ای بده، که بحثی در نگیره، کسی یک موقع به کسی سیخونک نزنه. چون پاش بیوفته خیلی از آدم‌ها می‌تونن جواب بدن، خیلی‌ها نمی‌تونن جواب بدن که چرا ریاضیات من مهمه. و ما برای همین هم توی خیام خیّام اصلاً یک سری دوم داریم که می‌گه چرا ریاضیات من مهمه؛ که یک نفر، یک ریاضی‌دان، باید بتونه جواب بده. مثلاً خیلی از ترکیبیات‌دان‌ها گراف کار می‌کنن می‌گن گراف مهمه به خاطر علوم کامپیوتر. می‌گیم چه گرافی داره؟ می‌گن گراف اینترنت. بعد می‌گیم خب بیاییم مقاله‌های شما رو ببینیم می‌گن که خب ما فعلاً قضیه‌هامون رو برای گراف منظم پنج راسی و شش راسی ثابت کردیم، یک گرنت گنده می‌گیرن برای هفت راسی و هشت راسی. آخه این چه ربطی به گراف اینترنت داره، این که نشد دلیل. و در جبر جابجایی هم عین همین هست. و ما باید یک مثلا انجمن ریاضی‌ای داشته باشیم، یا INSF مون، Iranian National Science Foundation مون یه همچین وظیفه‌ای رو به عهده بگیره، یا IPM مون این کار رو بکنه. که مدیریت تحقیقات ریاضیات رو به عهده بگیره، که تأیید کنه تحقیقات رو. مگه ما چقدر پول داریم؟ چقدر سرمایه داریم؟ چقدر آدم داریم؟ که هرکی بیاد رندوم هر کار خودش دوست داره انجام بده. ما باید برنامه‌ریزی کنیم، همسو کنیم تلاش هامون رو که به سمت یک هدف مشخصی حرکت کنیم، پیشرفت کنیم، ما عقب افتادیم. و این‌جور علم انجام دادن شایسته ما که این‌قدر نیاز داریم به توسعه و بخصوص به توسعه ریاضیات و بخصوص به توسعه ریاضیات محض، شایسته‌ی ما نیست. و شما اگه ریاضی محض رو درست انجام ندین، که ندادیم، مثل امروز از حیض انتفاع می‌افته، هیچ‌کی بهش توجه نمی‌کنه، الان دیگه داره می‌میره. هیچ ریاضیات محضی مورد اقبال نیست؛ تازه ریاضی کاربردی‌اش هم در افول به سر می‌بره. یعنی الان دانش‌آموزان دبیرستانی‌مون هم به سختی حاضر میشن بیان مهندس بشن. چرا؟ چون  می‌گن ما باید پزشک بشیم. پول توی پزشکیه. بنابراین این‌ها مشکلات مهمیه تو جامعه ریاضی، اینکه ریاضیدان‌ها چه تأثیری بر جامعه‌شون میذارن، که حالا من این‌ها رو در بستر نقد و تشویق تحقیقات در جبر خدمت شما عرض کردم.

آرش رستگار- نظریه نمایش با هدف مطالعه یک گروه:

آقای نادری می‌پرسند که آیا این درسته که ما یک گروه رو برای اینکه مطالعه‌اش کنیم، بیاییم همه نمایش‌هاش رو مطالعه کنیم؟ عرض کنم که راجع به این باید یک مدتی صحبت کنم. داستان اینه که یک قضیه‌ای از نش هست که می‌گه هر منیفولد مثلاً فشرده N بعدی، توی R^(2n+1) مثلاً می‌نشینه. و بعد نمی‌دونم embedding اش چطور، نمی‌دونم immersion اش چطور، و مانند این. و بعد می‌گه که پس ما اگه زیر خمینه‌های R^n ها رو مطالعه کنیم، همه خمینه‌ها رو مطالعه کردیم. و بعد اون می‌گه که پس زیر شیءهای اشیاء ساده رو مطالعه کردن کار درستیه، کار اشتباهی نیست. مثلاً می‌گه گروه‌ها، هر گروه متناهی، زیرگروه یک Sn ایه گروه جایگشتیه، بنابراین می‌گه زیر گروه‌های گروه‌های جایگشتی، مطالعه همه گروه‌های متناهی رو توی خودشون دارن. و بعد می‌گه که خب ما نمایش گروه‌ها رو که بررسی می‌کنیم در واقع این‌ها رو داریم توی GLn ها، حالا با ضرایب توی حلقه‌های مختلف، می‌نشانیم. و بله با همون فلسفه این گروه‌ها رو می‌شه مطالعه کرد. خوب این نگاه خیلی نگاه درستیه اما به عنوان تنها نگاه برای بررسی مثلاً گروه‌ها و مطالعه شون که معرفی نشده؛ نگاه‌های دیگه‌ای هم هست. و اینکه این نگاه ببینیم میوه‌هاش چی بوده؛ مثلاً میوه‌هاش همون نظریهinfinite dimentional representaion of Lie Groups است که توی فیزیک به ما ذرات بنیادی رو داد، این همین نظریه هریش چاندرا رو به ما داد و بعد Langlands program رو به ما داد. بنابراین یک نگاه درست هم چقدر زاینده است و هم چقدر ایده‌های خوب به ما می‌ده، چیزای زیادی ازش یاد می‌گیریم، و هم اینکه خب این مادر هر بچه‌ای که نمی‌تونی بزاد، چینی که نمی‌تونه بزاد، سیاه‌پوست که نمی‌تونه بزاد، نمی‌دونم چشم آبی که نمی‌تونه بزاد؛ اون چیزهایی که تو ژن‌اش هست می‌تونه بزاد. بنابراین ما باید روی مادرهای دیگه هم سرمایه‌گذاری کنیم؛ نمی‌شه گروه‌ها رو فقط با نمایش‌هاشون مطالعه کنیم.